The basic idea behind this kind of analysis is that there are certain latent topics in a body of text. Some words like car and automobile have a very similar meaning which means they are used in similar contexts. There is a lot of redundancy in language, and with enough effort you can group similar words together into topics.

Math behind the idea

Words are represented as vectors (see vector space model), which are a combination of direction and magnitude. Each word starts out pointing to its own dimension with magnitude 1, which means there is a huge number of dimensions (maybe hundreds of thousands, one for every word that comes up in the data set you’re working on). The basic problem is to flatten these large number of dimensions into a smaller number which are easier to manage and understand.

These vectors are represented as a matrix. In linear algebra, there is the idea of a basis, which is the set of vectors that describe the space you’re working in. For example, in everyday 3D space your basis would have one vector pointing in each dimension.

For another example, you could have a basis which is two vectors that describe a 2D plane. This space can be described in 3 dimensions, like how a piece of paper exists in the real world. But if all you’re dealing with is a 2D plane, you’re wasting a lot of effort and dealing with a lot of noise doing calculations for a 3D space.

Essentially, algorithms that do latent analysis attempt to flatten the really large space of all possible words into a smaller space of topics.

A fairly good explanation of the math involved is in the ‘Skillicorn – Understanding Complex Datasets‘ book, in chapters 2 and 3.

For a Mahout example, see Setting up Mahout. There are also examples in the examples/bin directory for topic modelling and clustering.

Latent Semantic Indexing example

Mahout doesn’t currently support this algorithm. Maybe because it was patented until recently? Hard to parallelize? In any case, there’s a Java library called SemanticVectors which makes use of it to enhance your Lucene search.

Note: I think there’s a technical distinction between topic modelling and LSI, but I’m not sure what it is. The ideas are similar, in any case

It’s just a JAR so you just need to add it to CLASSPATH. However, you need to also install Lucene and have it in your CLASSPATH (both lucene-demo and lucene-core jars.)

• Index the Enron data (or some other directory tree of text files) into Lucene:  java org.apache.lucene.demo.IndexFiles -index PATH_TO_LUCENE_INDEX -docs PATH_TO_ENRON_DOCS
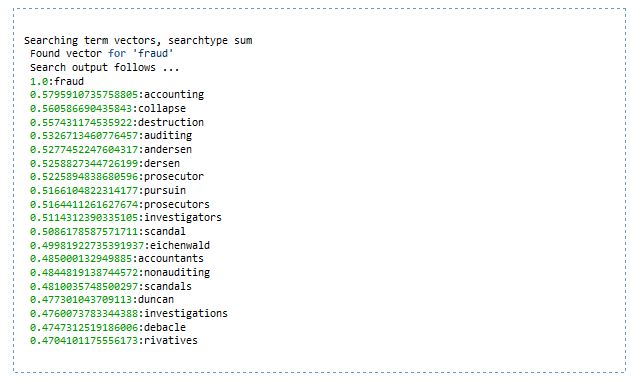
• Create LSI term frequency vectors from that Lucene data (I think this took a while, but I did it overnight so I’m not sure): java pitt.search.semanticvectors.BuildIndex PATH_TO_LUCENE_INDEX 
• Search the LSI index. There are different searchtypes, I did ‘sum’, the default: java pitt.search.semanticvectors.Search fraud

Here’s my result:

The input is fairly dirty. Mail headers are not stripped out and some emails are arbitrarily cut up at the 80th column (which may explain ‘rivatives’ at the bottom instead of ‘derivatives’). Still, it can be pretty useful